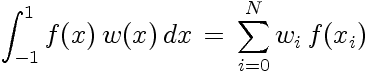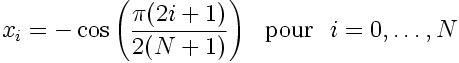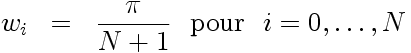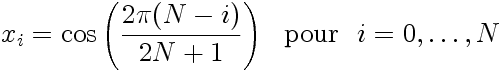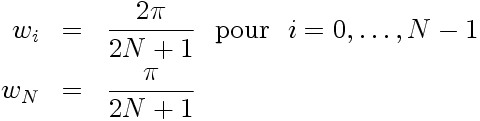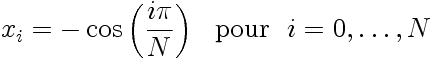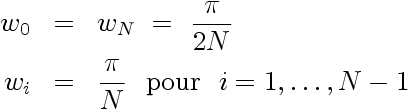Associées aux polynômes
de Tchebychev
1. Quelques mots sur la quadrature
La décomposition d'une fonction sur des polynômes
orthogonaux demande d'évaluer des produits scalaires.
Ces produits prennent la forme d'intégrales d'une fonction
f(x) (qui n'est a priori connue qu'au travers des valeurs qu'elle
prend en N+1 points) par une fonction poids w(x) connue.
On sait par ailleurs évaluer, de manière exacte,
une telle intégrale, à condition que f(x) soit un
polynôme de degré au plus égal à N
(ainsi que relaté dans la page consacrée
à
l'intégration
numérique), et ceci quel que soient les abscisses
x
i employées. Partant de ce constat,
on peut se demander si il n'existe pas quelques jeux de points
particuliers sur lesquels l'évaluation numérique de
l'intégrale soit exacte pour des polynômes de degré
supérieur à N.
Une telle optimisation est effectivement possible;
c'est la quadrature de Gauss décrite ci-dessous.
2. Poids des quadratures et points de collocation
associés
Le but de la manœuvre est de déterminer
les abscisses x
i et poids
w
i tels que la relation
soit exacte lorsque f(x) est un polynôme de degré le plus
élevé possible.
Remarque:
- Dans le cadre d'un développement sur les polynômes
de Tchebychev, la fonction "poids" dans l'intégrale
est w(x) = (1-x2)-1/2. Les
w i apparaissant dans la somme
sont, par analogie, qualifiés
de "poids de la quadrature".
La quadrature la plus performante est celle de Gauss: sur le jeu
de points de collocation associé,
la somme pondérée est exacte
(c.-à-d. égale à l'intégrale)
pour des polynômes de degré allant jusqu'à
2N+1. Il en existe deux autres,
les quadratures de Gauss-Radau et Gauss-Lobatto, qui, bien que techniquement
légèrement inférieures, sont également
particulièrement utiles.
2.1. Quadrature de Gauss
En décomposition Tchebychev,
la quadrature de Gauss, exacte pour des polynômes
de degré 2N+1 ou moins, impose que les
points de collocation soient les zéros de T
N+1(x).
Ces points sont:
Et les poids de cette quadrature sont alors:
2.2. Quadrature de Gauss-Radau
En décomposition Tchebychev,
la quadrature de Gauss-Radau, exacte pour des polynômes
de degré 2N ou moins, impose que les
points de collocation soient les zéros de
T
N+1(x) - T
N(x).
Ce qui implique les abscisses:
Et les poids associés à cette quadrature sont alors:
Remarque:
- Le jeu de points de Gauss-Radau donné ci-dessus
inclue la frontière x N
= 1.
Il est possible d'utiliser un jeu miroir
qui incluerait l'autre frontière du domaine.
2.3. Quadrature de Gauss-Lobatto
En décomposition Tchebychev,
la quadrature de Gauss-Lobatto, exacte pour des polynômes
de degré 2N-1 ou moins, impose que les
points de collocation soient les zéros de
(1-x
2).T
(1)N(x)
(T
(1)N désignant, évidemment,
la dérivée
première de T
N(x)).
Ces points ont pour abscisses:
Et les poids de cette quadrature sont alors: