Généralités
1. Polynômes orthogonaux et quadratures
Connaissant les valeurs prises par une fonction f(x) sur un jeu de (N+1) points de collocation xi, on peut construire un polynôme d'interpolation de degré N: PN(x). Disposant d'une base de polynômes orthogonaux Bk(x) (de degrés k), on peut développer PN(x) sur celle-ci; c'est-à-dire comme une somme pondérée des Bk(x):
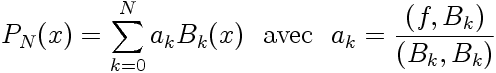
|
Où la notation (,) correspond à un produit scalaire discret entre les deux quantités concernées.
Sans rentrer dans les details, disons simplement que toute la difficulté de ce développement réside, une fois le jeu de polynômes orthogonaux choisi, dans l'évaluation des coefficients ak. La détermination de ceux-ci se ramène en fait à l'évaluation d'une intégrale impliquant f(x) (généralement inconnue). le problème se réduit alors à celui de l'utilisation d'une quadrature (c.-à-d. de déterminer l'intégrale en tant que somme pondérée de f(x) aux points de collocation) aussi efficace que possible.
Le choix d'une quadrature optimale (telles que celles de Gauss, Gauss-Radau et Gauss-Lobatto qui seront présentés plus bas) impose l'utilisation de jeux de points de collocation bien précis.
2. Généralités et propriétés principales des polynômes de Tchebychev
Les polynômes de Tchebychev (de première espèce) Tk(x), sont tels que:|
|
Les Tk(x) sont des polynômes de degrés k, liés par triplets par récurrence:
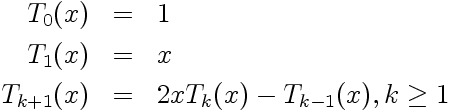
|
Ces polynômes sont, sur l'intervalle [-1;1] et vis-à-vis de la fonction poids w(x) = (1-x2)-1/2, orthogonaux:
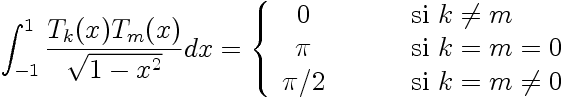
|
3. Quadratures et points de collocation associés aux polynômes de Tchebychev
Ayant choisi d'employer les polynômes de Tchebychev comme base de polynômes orthogonaux de travail, il reste à choisir la quadrature à employer (quadrature qui, rappelons le, fixera en conséquence les points de collocation à utiliser).Les trois quadratures les plus optimales (plus à ce propos) sont:
La quadrature de Gauss, qui implique le jeu de points de collocation:
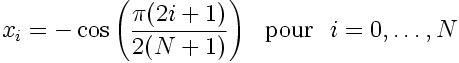
|
Remarques:
- Ces points sont irrégulièrement répartis sur l'intervalle [-1;1]. Ils sont plus espacés vers le centre du domaine et d'autant plus resserés qu'ils approchent des bornes de celui-ci (l'espacement entre points consécutifs, au voisinage de -1 et 1, est proportionel à 1/N2 ).
- Les deux bornes de l'intervalle (-1 et 1) ne font pas partie de ce jeu de points de collocation.
- Ces points sont symétriquement répartis autour de 0 (c.-à-d. tels que x i = x N-i ).
La quadrature de Gauss-Radau, qui implique le jeu de points de collocation:
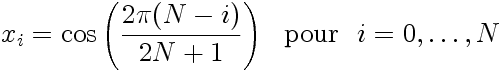
|
Remarques:
- Comme les points de Gauss, ces points sont irréguliérement répartis sur l'intervalle [-1;1] et d'autant plus resserés qu'ils se trouvent proche des bornes de celui-ci.
- Une borne de l'intervalle, x N = 1 est comprise dans ce jeu de points de collocation. Il est possible de construire un jeu de points alternatifs (miroir de celui donné ici) qui incluerait la borne -1.
La quadrature de Gauss-Lobatto, qui implique le jeu de points de collocation:
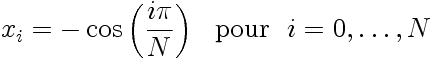
|
Remarques:
- A nouveau, ces points sont irréguliérement répartis sur l'intervalle [-1;1] et d'autant plus resserés qu'ils se trouvent proche des bornes de celui-ci.
- Les deux bornes de l'intervalle, x 0 = -1 et x N = 1 font partie du jeu de points de collocation.
- Comme ceux de Gauss, ces points sont symétriquement répartis autour de 0 (c.-à-d. tels que x i = x N-i )
4. Représentation d'une fonction sur les polynômes de Tchebychev
Sur (N+1) points de collocation répartis sur l'intervalle [-1;1], le polynôme d'interpolation fN(x) d'une fonction f(x) est:
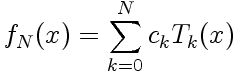
|
Connaissant les valeurs prises par f(x) aux points de collocation xi, yi = f(xi), on voit que la relation ci-dessus peut s'écrire sous la forme d'un produit matrice vecteur: P.c = y, où c est le vecteur des coefficients spectraux ck et P est la matrice de passage dont les éléments sont Pi,j = Tj(xi).
En d'autres termes, connaissant les valeurs nodales yi, on a accès aux coefficients spectraux ci (par multiplication du vecteur y par l'inverse de P) et réciproquement.
Terminologie:
-
On qualifie la matrice P de matrice de passage de l'espace
spectral à l'espace physique (puisque sont application sur les
coefficients spectraux permet d'obtenir les valeurs nodales).
Son inverse, P -1, permettant l'opération
inverse (l'obtention des coefficients spectraux à partir des
valeurs nodales), est qualifiée de matrice de passage
de l'espace physique à l'espace spectral.
Description détailée de ces matrices.