Matrices de dérivation
1. Brève introduction
Connaissant les (n+1) valeurs y i = f(x i) prises par une fonction (généralement inconnue) aux points de collocation x i, on souhaite évaluer les dérivées de cette fonction en ces mêmes x i.A l'aide du polynôme d'interpolation de Lagrange, construit sur les x i, on peut obtenir les y i(d) (c.-à-d. les valeurs de la dième dérivée aux points de collocation); ce qui s'écrit sous la forme du produit matrice vecteur: D n(d)×y(d) = y où y(d) et y sont les vecteurs contenant les y i(d) et y i et D n(d) est la matrice de dérivation dième (lien vers la page traitant de ce sujet).
Dans le cas de points de collocation équidistants x i = x 0 + i.h, ces matrices de dérivation ne dépendent plus que de h, le pas (la taille de l'intervalle) entre points successifs.
2. Expressions des matrices de dérivation première et seconde pour n=2
En substituant x i = x 0 + i.h dans les expressions générales des matrices de dérivation correspondantes, on obtient les expressions de D 2(1) et D 2(2) suivantes:
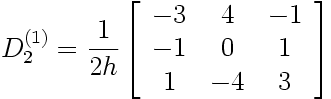
|
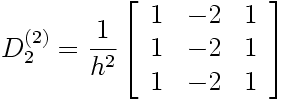
|
3. Expressions des matrices de dérivation première et seconde pour n=3
Après substitution, la matrice de dérivation première D 3(1) est:
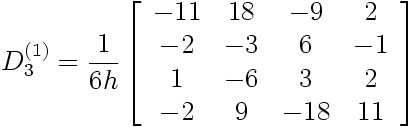
|
et la dérivée seconde D 3(2):
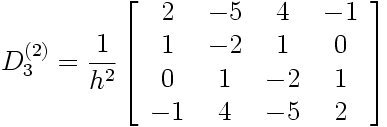
|
4. Expressions des matrices de dérivation première et seconde pour n=4
Pour 5 points, on obtient D 4(1):
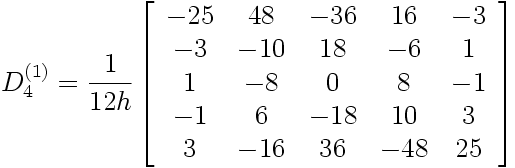
|
et D 4(2):
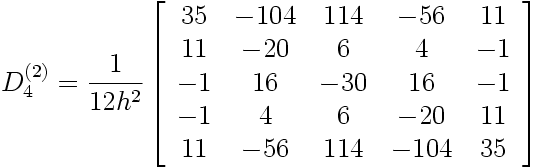
|
Petit formulaire (fichier PDF, 4 pages, 44k) comprenant l'expression de ces matrices.