Méthode des différences finies

1. Contexte

Résoudre numériquement une équation différentielle consiste à approximer, le plus précisément possible, la solution en un certain nombre de points (les points de collocation). On construit ainsi un système (linéaire) liant, via l'approximation numérique des dérivées concernées, les valeurs nodales (les valeurs de la solution numérique aux points de collocation) entre elles.
L'idée maîtresse sur laquelle repose cette approche est que, la solution approchée (celle obtenue aux points de collocation) tend vers la solution exacte du problème différentiel traité, l'approchant d'autant mieux que le nombre de valeurs nodales résolues est grand.

2. Procédure pour la résolution d'une équation différentielle avec conditions aux limites

La résolution numérique d'une équation différentielle linéaire, avec conditions aux limites, se résume à trois grandes étapes:

1. La discrétisation du problème, c'est à dire le choix des points de collocation sur lesquels sera approximé l'équation différentielle ainsi que le type d'approximation numérique des dérivées en ces mêmes points. On obtient ainsi un système linéaire liant les valeurs nodales entre elles.
2. La prise en compte des conditions aux limites du problème: Au même tître que celles-ci complètent l'équation différentielle, leurs approximations numériques, injectées dans le système linéaire (relatif aux valeurs nodales) complètent ce dernier.
3. La résolution du système linéaire liant les valeurs nodales entre elles.

Pour illustrer cela, considérons l'équation différentielle d'ordre deux suivante: Où les fonctions a₂(x), a₁(x), a₀(x) et S(x) sont données (les jeux de conditions aux limites associés, et leur traitement, est discuté plus loin).
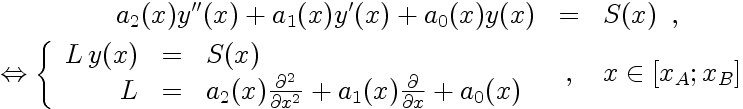
Ayant choisis un ensemble de m+1 points de collocation x _i (répartis sur l'intervalle [x ₀ = x _A; x _m = x _B] ), on construit le système linéaire liant les valeurs nodales y _i = y(x _i); système matriciel de la forme L.y = S, où y est le vecteur contenant les valeurs nodales y _i , S le vecteur source dont les éléments sont les S(x _i) et la matrice L l'opérateur traduisant l'action de l'opérateur différentiel L aux valeurs nodales.

2.1. Construction du système linéaire. Utilisation de stencils et des matrices de dérivation associées

La transcription de l'action de l'opérateur différentiel L aux m+1 points de collocation implique que les éléments de la matrice L sont donnés par: L _ij = a₂(x _i) d _ij⁽²⁾ + a₁(x _i) d _ij⁽¹⁾ + a₀(x _i) d _ij⁽⁰⁾ , où d⁽²⁾, d⁽¹⁾ et d⁽⁰⁾ sont les matrices de dérivation seconde, première et zéro-ème (donc la matrice identitée).
Tout va donc reposer sur l'écriture des matrices d⁽²⁾ et d⁽¹⁾, c'est à dire des hypothèses (et contraintes résultantes) du degré d'approximation pris en compte.
En ce qui concerne la méthode dite des différences finies, on fait le choix d'utiliser des approximations locales à chaque point de collocation. A l'aide de quelques points voisins, on construit un polynôme d'interpolation qui permet d'évaluer la valeur de la dérivée au point de collocation, en fonction des valeurs nodales voisines. En pratique, on utilise des stencils de trois ou cinq points, qui correspondent à des approximations d'ordre 2 ou 4. Les matrices de dérivation correspondantes sont donné dans la page traitant de ce sujet. Sachant de plus, que les stencils décentrés sont généralement moins précis que leurs homologues centrés (c.-à-d. où la dérivée est évaluée grâce aux valeurs nodales de points encadrant au mieux le point de collocation considéré). Ce n'est qu'au voisinage des bornes du domaine où, faute de mieux, on a recours aux stencils décentrés.

2.2. Prise en compte des conditions aux limites

Le système linéaire L.y = S ne rend compte que de l'équation différentielle étudiée. Or, celle-ci est assortie de conditions aux limites qu'il faut également retranscrire. Du point de vue du système linéaire, cela signifie que l'on dispose de deux contraintes complémentaires (sur les valeurs nodales y₀ et y_m) à satisfaire. Ces contraintes, qui satisfont l'équation différentielle, sont à substituer aux expressions générales déduites ci-dessus. En clair, on remplace les équations relatives à y₀ et y_m (première et dernière lignes de la matrice L) par celles traduisant la discrétisation des conditions aux limites du problème.
Suivant la forme des conditions aux limites du problème à traiter, on distingue les types suivant:

Conditions aux limites de type Dirichlet
Les valeurs aux limites sont des données du problème: y(x_A) = y_A et y(x_B) = y_B qui implique directement que les valeurs nodales y₀ = y_A et y_m = y_B sont connues. On peut donc aisément réécrire le système L.y = S (système (m+1)×(m+1)) sous une forme plus réduite (système (m-1)×(m-1)) ne portant sur les valeurs nodales intérieures y_i, i = 1,...,m-1.

Conditions aux limites de type Neumann
Les valeurs des dérivées (premières) aux limites sont des données du problème: y'(x_A) = y'_A et y'(x_B) = y'_B. A partir des matrices de dérivation (des stencils employés), on dispose des relations entre y'₀ = y'_A en fonction de y₀, y₁, y₂, ... et y'_m = y'_B en fonction de y_m, y_m-1, ..., qui sont à insérer dans les première et dernière lignes de la matrice L.

Conditions aux limites mixtes
Les valeurs aux limites et leurs dérivées sont donnéees par une relation linéaire entre elles, du type c_A y_A + k_A y'_A = q_A; c_A, k_A et q_A étant des constantes connues. A l'aide de la matrice de dérivation (du stencil employé), cette relation se discrétise aisément et conduit à une relation entre y₀ = y_A et les valeurs nodales voisines y₁, y₂, ... qu'il suffit d'insérer dans (la première ligne de) L. Ce type de condition aux limite, expriméee en l'autre borne du domaine x _m, se traite évidemment de même et conduit similairement à réécrire la dernière ligne de L.

2.3. Résolution du système linéaire

Une fois le système linéaire construit, il n'y a plus qu'à le résoudre (c.-à-d. à résoudre via votre solver linéaire préféré) pour connaître les valeurs nodales y_i recherchées.
La résolution numérique de systèmes linéaires n'étant pas le sujet de cette page, ce sera tout à ce propos, si ce n'est la remarque suivante: Les matrices de dérivation résultant de la formulation différences finies sont des matrices creuses à bande unique autour de la diagonale (typiquement, elles sont tridiagonales pour des stencils d'ordre 2 et pentadiagonales pour des stencils d'ordre 4), ce qui permet l'emploi de méthodes de résolution spécifiques et performantes pour la résolution du système.

3. Un exemple pour illustrer la procédure

Pour clarifier la procédure et illustrer sa mise en œuvre, voir les pages suivantes: Résolution d'un exemple simple, sur des points de collocation équidistants, par différences finies d'ordre 2 et par différences finies d'ordre 4.