Exemple: Utilisation des différences finies d'ordre 2

1. Contexte - Exemple traité

Soit à résoudre l'équation différentielle:
Et ce, dans le cadre des trois jeux de conditions aux limites, de type Dirichlet (D), Neumann (N) ou mixtes (M):
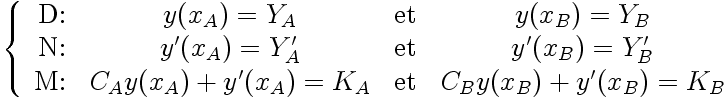
Afin d'illustrer la procédure générale, on se focalise ici sur la résolution du problème sur 8 points de collocation x _i équirépartis sur l'intervalle.
En clair, on aura ici x ₀ = x _A = -1 , x ₇ = x _B = +1  et conséquemment x _i = x ₀ + i.h (pour i = 0,...,7), avec h = (x _B - x _A) / 7 = 2 / 7.

2. Discrétisation de l'équation différentielle

2.1. Utilisation des stencils pour construire les matrices de dérivation étendues

Sur trois points équidistants (espacés d'un pas h), les matrices de dérivation liant trois valeurs nodales consécutives {y _i-1, y _i, y _i+1} et leurs dérivées nodales (première et seconde) sont:
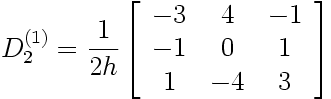
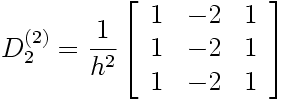
Ces stencils de base vont servir à construire les matrices de dérivation étendues d ₂⁽¹⁾ et d ₂⁽²⁾:
Sachant qu'une meilleure approximation est généralement obtenue via un polynôme d'interpolation centré, on utilise celle-ci autant que possible.
Ainsi, la dérivé première en x _i est, dès que possible, déduite de la relation y' _i = (1/2h).(-1.y _i-1 +0.y _i +1.y _i-1) donnée par l'application de la matrice D ₂⁽¹⁾ au (sous-)vecteur (y _i-1, y _i, y _i+1). Ce n'est qu'au voisinage des frontières qu'il faut recourir aux approximations décentrées. Pour cet exemple, cela signifie que y' ₀ = (1/2h).(-3.y ₀ +4.y ₁ -1.y ₂) (déduit de la première ligne du système resultant de l'application de D ₂⁽¹⁾ au (sous-)vecteur [y ₀, y ₁, y ₂]. De même, la dernière ligne du système résultant de l'application de D ₂⁽¹⁾ au (sous-)vecteur [y ₅, y ₆, y ₇] implique y ₇' = (1/2h).(1.y ₅ -4.y ₆ +3.y ₇).
En regroupant toutes ces relations, on obtient la matrice de dérivation (première) étendue d ₂⁽¹⁾:
En procédant de manière identique vis-à-vis des dérivées secondes, à l'aide de D ₂⁽²⁾, on construit d ₂⁽²⁾:

2.2. Construction de l'opérateur différentiel L

Les éléments de l'opérateur différentiel sont ici simplement:
L _ij = d_2 ij⁽²⁾ + 2 d_2 ij⁽¹⁾ - 3 d _ij⁽⁰⁾
Où, pour mémoire, d⁽⁰⁾ n'est rien d'autre que la matrice identité.
Au final, la version discrétisée de l'équation différentielle L.y = S est donc:

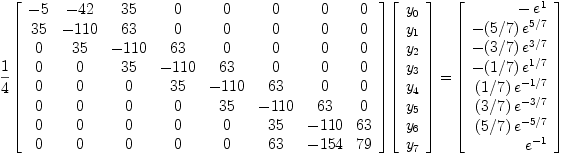
3. Prise en compte des conditions aux limites

Imposer les conditions aux limites du problème aux noeuds x ₀ et x ₇ impose de réécrire les première et dernière lignes du système discrédisé.

3.1. Conditions aux limites de type Dirichlet

Les valeurs nodales y ₀ = y(x _A) = Y_A et y ₇ = y(x _B) = Y_B sont connues, ce qui permet de réécrire le système reduit aux seules valeurs nodales inconnues:

3.2. Conditions aux limites de type Neumann

Seules les valeurs des dérivées aux frontières sont connues: y'(x _A) = Y'_A et y'(x _B) = Y'_B.
D'après D ₂⁽¹⁾, appliqué au (sous-)vecteurs [y ₀, y ₁, y ₂] et [y ₅, y ₆, y ₇], on déduit les relations à satisfaire aux frontières:
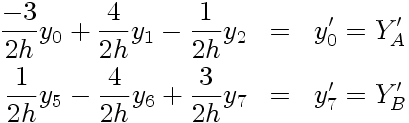
Et le système linéaire devient donc:

3.3. Conditions aux limites mixtes

On dispose des relations aux frontières: C _A y(x _A) + y'(x _A) = K _A et C _B y(x _B) + y'(x _B) = K _B , où C _A, K _A, C _B et K _B sont des constantes connues. En utilisant (comme pour le cas Neumann décrit ci-dessus) D ₂⁽¹⁾ pour exprimer les valeurs de y' ₀ et y' ₇ en fonction des valeurs nodales voisines, on obtient les relations:
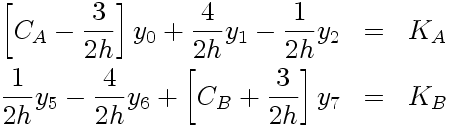
Et le système linéaire devient alors:

4. Remarques et autres compléments

• Document récapitulatif (fichier PDF,5 pages, 53k) de cet exemple, illustrant également la procédure pour un traitement du problème à l'ordre 4.
• Les systèmes linéaires obtenus dans les cas de conditions aux limites de type Neumann et mixte sont quasi-tridiagonaux: les première et dernière lignes contiennent trois termes. On peut facilement les mettre sous forme tridiagonale (en particulier si l'on souhaite utiliser un solver spécifique à ce type de systèmes) en se débarassant des termes offensants par élimination Gaussienne. Pour l'exemple ci-dessus, il faudrait ainsi ajouter (-L _0 2 /  L _1 2 =) 7/63 fois la deuxième ligne de L à la première et de même ajouter (-L _7 5 /  L _6 5 =) -7/35 fois l'avant-dernière ligne à la dernière (et ne pas oublier de faire subir ces mêmes transformations aux second membre).
• L'extension de ces procédures à un nombre plus important de points de collocation est immédiate.
• La discrétisation (et résolution) du problème pour des jeux de points de collocation non-équidistants suit exactement le même chemin, le seul petit travail supplémentaire concernant l'emploi de stencils (et matrices de dérivations correspondantes) variant celon la valeur nodale autour de laquelle on les applique.